In astronomy, we often describe the size of celestial objects, or the spacing between them, using a measurement called angular separation.
The units of measure may look familiar: degrees, minutes, and seconds of arc. (For a detailed explanation, see this article.) It seems natural to wonder if we can convert these measurements into more familiar units of distance such as feet, meters, miles, or kilometers.
The short answer is: not really, though there are certain exceptions. The main advantage of using degrees, minutes, and seconds of arc to describe the size and position of objects is that they ignore actual distances and instead describe apparent distance.
Once you are familiar with the usage of these units, you can get a sense of how large an object will appear, or how far it will be from some other object, without requiring any knowledge of that object’s physical properties such as its actual distance or diameter.
The conversion we want to make is from angular distance to linear distance. Arc-Minutes are expressed in degrees which do not directly correlate with any regular distance.
But what if you want to calculate the physical properties of an object, like size or distance?
Can this be done from the apparent size alone?
Not really. The best way to learn about the size of an object you are viewing is to read about it. Wikipedia is a fine start. Free planetarium apps such as Sky Safari and Stellarium contain detailed information on thousands of objects. There are a lot of ways that you may use arc-seconds and arc-minutes in astronomy, read more about the measurements in this post.
I also like to keep reference guides such as the Concise Catalog of Deep-Sky Objects around when observing.
The more you know about what you are observing the more you will enjoy observing.
This is not to say that it is impossible to convert arc-minutes to meters.
To convert arc-minutes to meters you need to know the distance to the object you are viewing. More precisely, you need to know the radius of an imaginary sphere, if you are at the sphere’s center and the object of interest is fixed on the sphere’s circumference. From there, it is relatively simple to calculate the object’s actual diameter; in fact, the nautical mile was originally defined by this method, corresponding to one minute of arc at sea level along Earth’s equator.
As a tool for calculating astronomical distance, it is still a lot faster to use your search engine.
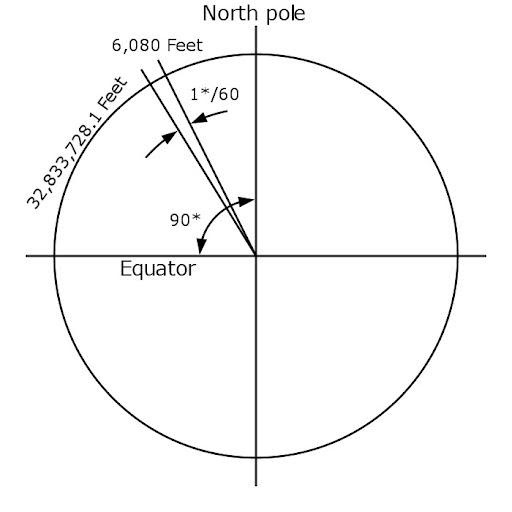
Nautical Mile
In principle, you could calculate the actual diameter of objects whose distance is precisely known, such as lunar craters.
In addition to the Earth-moon distance, you would need to approximate the angular size of the feature in question, after which you could use the formula:
s=Rθ
where s is the size of the object (technically the arc length), R is the distance to the object (that is, the radius of your imaginary sphere), and θ is the angular size of the object (in radians, not degrees).
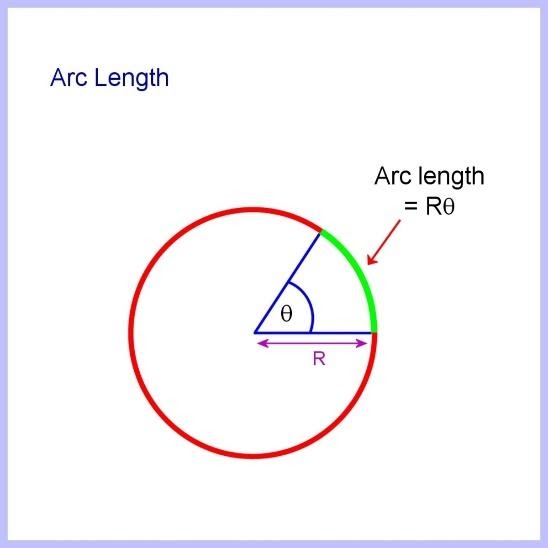
If that seems overly complicated for something you could just as easily Google in eight seconds, well, I won’t disagree with you.
Minute of Arc
One place you will see conversion from angular size to linear distance is in sporting optics: think binoculars, spotting scopes, and rifle scopes.
Such instruments often express their fields of view in linear terms instead of, or in addition to, angular field of view.
You’ll notice that the linear field of view is always given at a specified distance, such as 100 yards.
In fact, target shooting relies on the relationship between angle and distance to account for bullet drop while aiming. The term you will see is minute of arc (MOA), where 1 MOA is rounded off to 1 inch per one hundred yards (the actual figure is 1.047”). From there we can just multiply: one arc-minute is equal to about 5.25” at 500 yards, 10.5” at 1000 yards, and so on.
Astronomical instruments, on the other hand, have no use for linear field of view, since actual distances to your target objects vary enormously and are usually based on estimates anyway, rather than measured distances.
Converting arc-minutes to meters, or any other angular-to-linear conversion, serves little purpose in recreational astronomy.
In the science of astronomy, it is a different story. Parallax angle is used to accurately measure the distances to nearby stars.
You can see how this works by extending your hand and holding your thumb up. Alternate between having your left and right eyes closed, and you will see the apparent position of your thumb change relative to objects in the background.
This effect is called parallax. By measuring the distance between your eyes, and figuring out the angular shift of your thumb, you can then use a bit of trigonometry to calculate the distance between your thumb and your face.
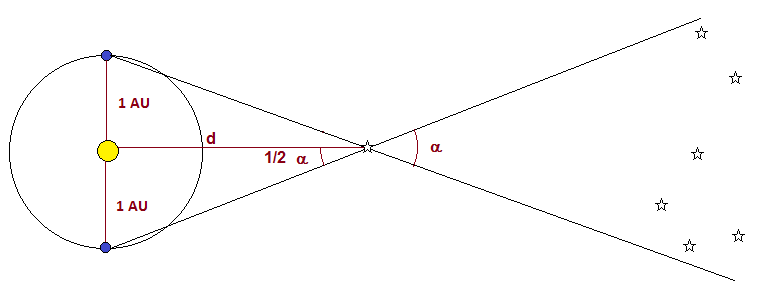
Because even the closest stars are so far away, the distance between your eyes isn’t enough to create a detectable parallax effect. Instead, astronomers take measurements six months apart, when the Earth is at opposite sides of the sun.
Now we finally have an angle which, while still incredibly small, we can work with, provided the star is not too far away.
When the parallax angle of a star is equal to one arc second, we call this distance one parsec, equal to 3.26 light years.
The formula is simply:
d=1/p
Where d is the distance to the star in parsecs, 1 is the Earth-sun distance in astronomical units, and p is the parallax angle.
We can see that smaller angles equal greater distances.
While it might not be possible to convert angular measurements directly into linear distance, angles are still incredibly useful in astronomy for mapping out our nearby universe.
You can measure these distances with your hand and they are the language of astronomical measurement. I have written a simple guide to these measurements that you can find here.